The possible states of the energy of electrons in an atom are numbered by the well-known quantum numbers $n$, $l$, $m$ and $s$ Some nuclei of atoms, for example the atom $^ 1H$ (normal isotope of hydrogen) can also take different energy states provided they are subjected to an intense magnetic field. In contrast with the atomic energy levels, these levels depend on the intensity of the magnetic field to which the nuclei are subjected. The nucleus $^ 1H $ for example, can present two energy states when it is subjected to a magnetic field $ H $ and the energy difference $\Delta E$ between these two states increases, if we increase the magnetic field strength.
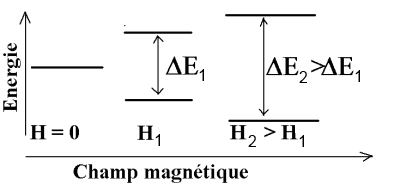
According to Planck's law, the nucleus $^1H $ - subject to a $H_1$ field absorbs electromagnetic radiation frequency $\nu_1$ $=$ $\frac{\Delta E_1}{h}$ (typically in the area of radio frequency) - subject to a $H_2$ field absorbs radiation of frequency $\nu_2$ $=$ $\frac{\Delta E_2}{h}$

But even if a strictly constant magnetic field is applied to a sample of material containing $^ 1H$ atoms, nuclei of all atoms will not be exposed to the same field because the external field will be modified by the electronic environment of these nuclei . According to this electronic environment, therefore it should be noted that a different frequency radiation will be absorbed! This explains the possibility, by submitting the sample (in addition to the constant magnetic field) to increasing radio frequencies which will be more or less absorbed by $^1H$ atoms, to record spectra allowing to discern the $^1H$ atoms with a different electronic environment .
The external field of a nucleus is modified by the electronic environment of the nuclei. In "circulating" around the nucleus $^1H$, electrons create a field of opposite direction to the applied field (see physics: induction etc ..), thereby reducing the intensity of the applied field . $\Delta E$ is thus reduced and hence the frequency absorbed $\nu$: More a hydrogen nucleus is surrounded by electrons ("shielded"), the lower the radio frequency it will absorb!
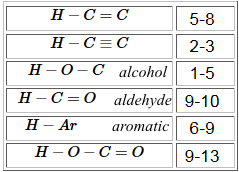
Chemical shift ( in $ppm$: parts per million ): $\delta=\frac{\nu - \nu_{ref}}{\nu_{ref}}\cdot 10^6$
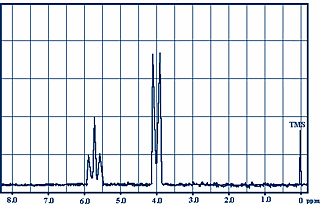
Here, for example, the NMR spectrum of the methyl ethanoate:

At $\delta = 0$, we find the absorption line of $H$ atoms of the tetramethylsilane which has been added to the sample, at $\delta= 2.00$ that of $H$ atoms of the methyl group $CH_3$ and at $\delta=3.65$ that of $H$ atoms of methoxy group $OCH_3$.
- The negative inductive effect $-I$ of highly electronegative atoms decreases inductive shielding and increases $\delta$ (See f.i. the effect of the O atom of group $OCH_3$ !) - The positive inductive effect $+I$ of strongly electropositive atoms or alkyl chains increases the shield and decreases $\delta$ (See f.i. the effect of the Si atom in tetramethylsilane!) - The mesomeric effect can have important influence.
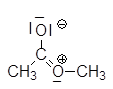
This contributive mesomeric structure with its positive charge on nitrogen certainly explains the large unshielding of $H$ atoms of the $OCH_3$ group!
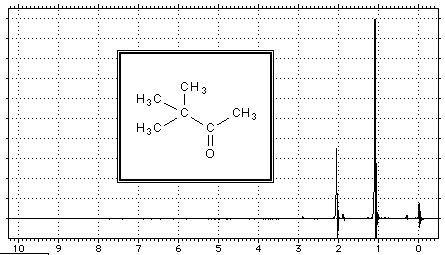
The 9 H atoms of the methyl groups on the left in the above example have a similar electronic environment (tetrahedral carbon structure, free rotation of the C-C bond). Peak $\delta = 1.1$ of these atoms has a surface 3 times larger than the peak at $\delta H = 2.05$ for the other methyl group. The peak area is proportional to the corresponding number of H atoms.
Consider the system consisting only of these three $H$ atoms :
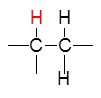
We know that the nucleus of each H atom can be in two states (energy levels). Refer to these states (spins) by +1/2 and -1/2. 1) What can "see" the left hydrogen in "watching" the two hydrogens on the right? (Even better: what is the influence transmitted by the electron clouds of $H$ on the right on the $H$ on the left?) Answer:

It will "see" three different configurations (1), (2) and (3) with the frequencies 1 : 2 : 1 ! Each of these configurations affects differently the chemical shift: Its peak will be split into a triplet! 2) What can "see" the right (equivalent) hydrogens in "looking" at the single left hydrogen ? Answer:
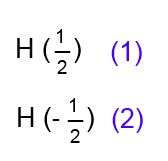
They "see" two different configurations (1) and (2) with frequencies 1: 1! Each of these configurations affects their chemical shift differently: Their peak will split into doublet! The total area of the triplet will be half that of the doublet, as the triplet is derived from one absorbing $H$, the doublet from two! In the triplet surfaces are in the ratio of frequencies 1: 2: 1!. In the doublet, the surfaces are in the ratio of frequencies 1: 1!.
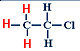
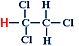
1,1,2-trichloroethane
Consider the system consisting only of these five $H$ atoms :

1) What can "see" each left hydrogen in "watching" the two hydrogens on the right? (Even better: what is the influence transmitted by the electron clouds of $H$ on the right to each left $H$ ?) Answer:

It will "see" three different configurations (1), (2) and (3) with frequencies 1: 2: 1! Each of these configurations affects differently the chemical shift: Their peak will split into triplet! 2) What can "see" the right (equivalent) hydrogens in "watching the three hydrogens on the left? Answer:

They "see" four different configurations (1) and (2) and (3) and (4) with frequencies 1: 3: 3: 1! Each of these configurations affects differently the chemical shift: Their peak will split into quadruplet!
The total area of the quadruplet will be two-thirds that of the triplet, since the triplet comes from three $H$ atoms which absorb while the quadruplet is derived from two! In the quartet, the surfaces are in the ratio of frequencies 1: 3: 3: 1!. In the triplet surfaces are in the ratio of frequencies 1: 2: 1!.

chloroethane