





The formation reaction of a substance is the chemical reaction which produces directly one mole of this substance from the usual elements.
$H_2$ $+$ $\frac{1}{2}O_2$ $\longrightarrow $ $H_2O$ is the formation reaction of water, but not: $2H_2$ $+$ $O_2$ $\longrightarrow$ $ 2H_2O$ , indeed: - $H_2$ et $O_2$ are the usual elementary substances. - but on the other side, the definition says that we must consider the reaction which forms one mole of the substance!
The standard enthalpy of formation of a substance is the enthalpy of its formation reaction.
At $25^oC$ and $1\;bar$ the reaction of $2 \;mol$ of hydrogen gas with $1\; mol$ of oxygen gas forming $2 \;mol$ of liquid water produces $571.66\; kJ$ : $2H_2(g)$ $+$ $O_2(g)$ $\longrightarrow$ $2H_2O(l)$ $\Delta H$ $ = $ $- 571.66 \;kJ$ Standard enthalpy of formation of water = $\Delta H_f(H_2O)$ $=$ $\frac{571,66}{2}$ $=$ $ - 285.83\;kJ$ !!
The standard enthalpies of formation of the usual substances have been determined. See the → Table They allow to calculate most "reaction heats " (= $-\Delta H_{reaction}$) and "transformation heats" (= $-\Delta H_{transformation}$):
$2H_2O(g)$ $+$ $2Cl_2(g)$ $\longrightarrow$ $4HCl(g)$ $+$ $O_2(g)$
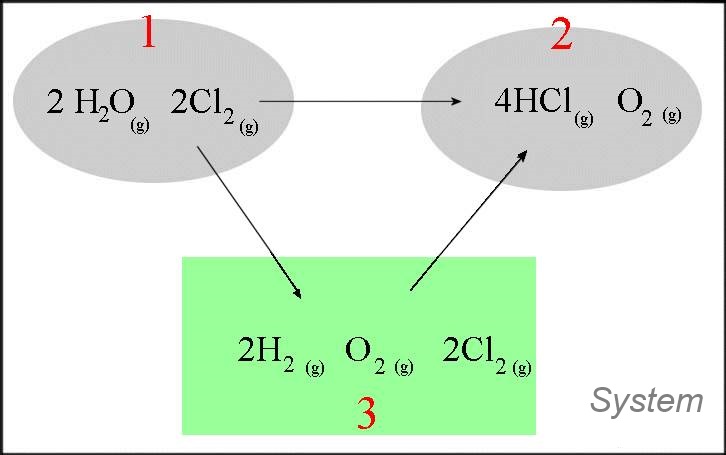
- In the green box are elements in their normal state - The transformations $3\rightarrow 1$ and $3\rightarrow 2$ are formation reactions ! $\Delta H_{12}$ $=\Delta H_{13}$ $+$ $\Delta H_{32}$ $=\Delta H_{32}$ $-$ $\Delta H_{31}$ $=(4\Delta H_f(HCl(g))$ $+$ $\Delta H_f(O_2(g)))$ $-$ $(2\Delta H_f(H_2O(g))$ $+$ $2\Delta H_f (Cl_2(g)))$ $=(-4\cdot92.31$ $+$ $0)$ $-$ $(-2\cdot 241.82$ $+$ $2\cdot 0)$ $=114.4\;kJ$ The enthalpy of this stoichiometric reaction at $298\;K$ and $1\; bar$ equals $114.4\;kJ$. The stoichiometric reaction at $298\;K$ and $1\; bar$ absorbs therefore $114.4kJ$ heat. The (stoichimetric) "reaction heat" at $298\;K$ and $1\; bar$ equals $-114.4kJ$.
We have seen a useful property in this example :
During a chemical reaction: $\Delta H(reaction)$ $ =$ $ \Sigma \Delta H_f(products)$ $-$ $\Sigma \Delta H_f(reagents)$ ($\Sigma$ = Sum)
$2H_2O(g)$ $\longrightarrow$ $2H_2O(l)$
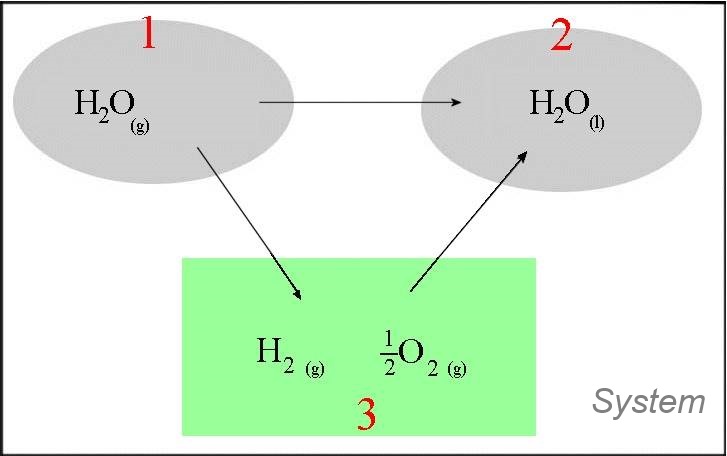
- In the green box are elements in their normal state - The transformations $3\rightarrow 1$ and $3\rightarrow 2$ are formation reactions ! $\Delta H_{12}$ $=\Delta H_{13}$ $+$ $\Delta H_{32}$ $=\Delta H_{32}$ $-$ $\Delta H_{31}$ $=\Delta H_f(H_2O(l))$ $-$ $\Delta H_f(H_2O(g))$ $=-285.83$ $-$ $(-241.82)$ $=-44.01\;kJ$ The enthalpy of this stoichiometric reaction at $298\;K$ and $1\; bar$ equals $-44.01kJ$ The transformation of $1 mol$ water vapour to liquid water at $298\;K$ and $1\; bar$ liberates therefore $44.01\; kJ$ heat. The heat of condensation, at $298\;K$ and $1\; bar$ equals $44.01\;kJ$.
We have seen still another useful property in this example :
During a physical transformation of a substance from initial state a to final state b : $\Delta H_{physical \; transformation}$ $=$ $\Delta H_f(b)$ $-$ $\Delta H_f(a)$