The internal energy $U$

The (closed) system seen from outside

A system (for instance a cable-car) may have overall kinetic energy owing to its speed and potential energy owing to its height However, chemistry is rather interested in systems constitued by a set of substances inside of the container where they may react. Global parameters like the eventual speed of the container or its height above sea level have no direct interest in chemistry.

The (closed) system seen from inside

The system consisting of $2$ moles $H_2$ and $1$ mole $O_2$ NTP is able to exercise in that state much more work on the surroundings then after it has been transformed to 2 moles of water (think about an hydrogen engine!). Therefore there must exist parameters which determine the internal energy of such a system.

The internal energy $U$ of a (closed) system

The internal energy U of a chemical system at a point in time comes in fact from - the kinetic energy of all species, molecules, atoms or ions of the system - the potential energy contained in the chemical bonds. Consider such a bond like a coil spring, a times more "stretched" than othertimes, therefore having more energy!

Movement of molecules in the water

It appears much too hard to evaluate $U$ considering all movements and interactions of the enormous number of particles present in a chemical system ! But in principle the internal energy $U$ should be calculable by the system parameters $P$,$V$,$T$ and $n_i$. ($U$ is said to be a state function). As even that calculation is often too hard to make in pratice, one is reduced to study changes of $U$ when the system transits from one state to another. Chemical reactions may indeed be considered as a changeover from an initial state (the reagents) to a final state (the products).

The first principle of thermodynamics

Physics teach us that heat and work are two "equivalent" energy forms, that means that they can be transformed the one into the other. That's why they have the same physical unit: 1 Joule($J$) = 1 Newton $\cdot$ meter ($Nm$)

Changes of internal energy of a system

This fundamental law can be applied to chemical systems: When a system gains energy (when its internal energy increases), this energy must come from the surroundings in the form of heat and (or) work . If we call $Q$ and $W$ the heat and work received by the system, it follows that:

Remember that $\Delta U$ means $U_{final}$ $-$ $U_{initial}$ and is equal to the gain of internal energy. In case $\Delta U$ < $0$, the same formula means that, as internal energy decreases, this lost energy must be found in the surroundings in the form of heat and (or) work.

Heat and work exchanged by a chemical system with the surroundings are easily measured, therefore we can determine the change of internal energy of a chemical system during its transformation!

The work exchanged by the system

The work exchanged between a chemical system and its surrondings lies mostly in its volume changes. In the combustion engine of cars, the explosion of gases (= the system) provides work to the piston and drives the car (= the surroundings).

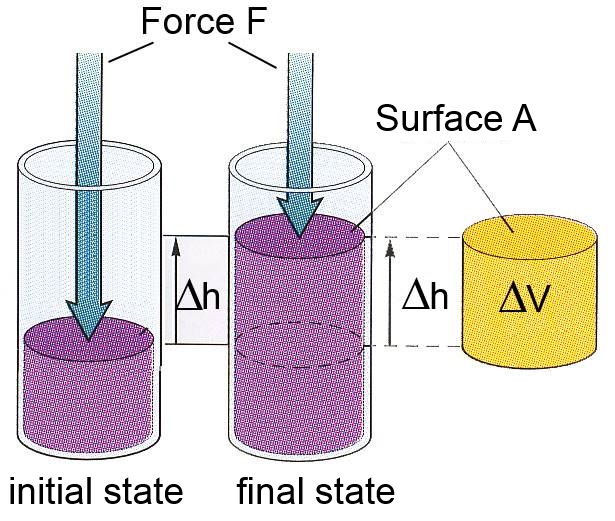
In most of chemical applications, the pressure remains constant during reaction (often the atmospheric pressure): Let's call this pressure $P$. Pressure is defined as $P$ $=$ $\frac{F}{A}$ The represented gas (system) expands gainst the constant force $F$ $=$ $P\cdot A$ and provides work to the surroundings $F\cdot\Delta h$ $=$ $P\cdot\Delta h\cdot A$ $=$ $P\cdot\Delta V$

The heat exchanged by the system

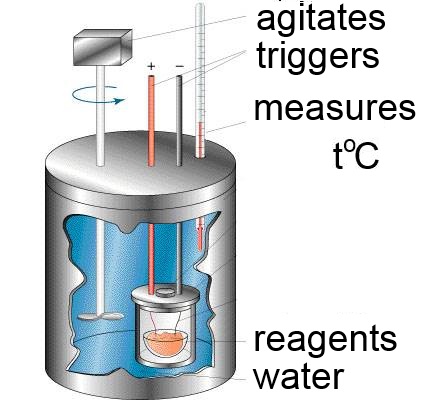
The heat exchanged by a system with its surroundings is measured in a calorimeter: S : The system of the reagents and their products. E : The water is part of the surroundings. It receives an amount of heat (in Joule) equal to $4184 \cdot m \cdot (\theta_f$ $-$ $\theta_i)$ where $4184 \frac{J}{kg \cdot K}$ is the specific heat capacity of water (= number of Joules needed to rise the temperature of $1\;kg$ water by $1\;K$) $m$ is the mass of the water (in $kg$) , $\theta_i$ the temperature in the beginning of the reaction, $\theta_f$ the temperature at the end of the reaction. C : The calorimeter too is part of the surrondings. It receives an amount of heat (in Joule) equal to $C\cdot (\theta_f$ $-$ $\theta_i)$ where $C$ is its heat capacity (in Joules per degrees)

It follows that:

Example 0.625 g de formaldehyde($H_2CO$) are burned for instance in an open calorimeter: $H_2CO+O_2$ $\longrightarrow$ $CO_2$ $+$ $H_2O$ The temperature of the water bath ($150\; g\;H_20$) rises from $24.0\; ^oC$ to $39.2\;^oC$. The heat capacity of the calorimeter equals $150 \frac{J}{K}$: $Q$ $=$ $-4184 \cdot 0.150 \cdot 15.2$ $-$ $150 \cdot 15.2$ $\approx$ $-11820 J$

Calorie and Joule

The calorie is an old heat unit:

Introducing in equation (2) and discarding the second term, we find: $1 cal$ $=$ $4184\cdot 0.001\cdot 1$ $=$ $4.184 J$

Very often the chemists prefer the calorie for heat unit and the gram for mass unit. In that case equation (3) becomes:

The determination of the variation of internal energy

If we manage to annullate the work $W$ received by the system in equation (2): $\Delta U$ $=$ $Q$ , the change in internal energy will be reduced to the heat received by the system which can be measured by calorimetry!! This requires, that changes of volume of the system (responsible in chemistry for the exchanged work with the surroundings) must be avoided, that is to say, that it must be operated at constant volume in a closed calorimeter ("=calorimetric bomb "):