





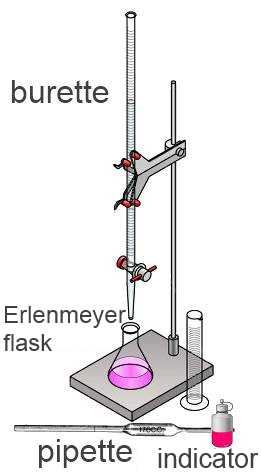
The solution to be titrated is a solution where the concentration of a solute 1 has to be found. The standard solution is a solution where the concentration of a reagent 2 is well known. Using a pipette a well defined volume $V_2$ of the solution 2 to be titrated ) is introduced in an Erlenmeyer flask. A few drops of a color indicator are added. While swirling around the Erlenmeyer, the standard solution is introduced up to when the indicator changes its color. At this moment the reaction is complete, no excess reagent has been added. The equivalent point is attained. The graduated burette indicates now the volume $V_1$ of standard solution 1 which was added.
The number of moles of reagent 1 are calculated by: $n_1=[1] \cdot V_1$ where $[1]$ is the molarity of reagent 1 Using the stoechiometry ( moles in the equation ) of the reaction, we may now calculate the number of moles $n_2$ of the substance 2 in the unknown solution. Then the molarity of the unknown solution is calculated by $[2]=\frac{n_2}{V_2}$
Question
A chemist has discovered a very curious element which he called "babaorum" (symbol $Bb$). He knows by some tests that $Bb$ is an alkaline earth metal. Its hydroxide would then have the formula $Bb(OH)_2$ and its reaction with chlorhydric acid would be noted: $Bb(OH)_2$ $+$ $2HCl$ $\longrightarrow$ $BbCl_2$ $+$ $2H_2O$ Our intrepid chemist weighs exactly $0.257 g$ of pure $Bb(OH)_2$, dissolves it in water and titrates by $HCl 0.2 M$. The equivalent point is attained after addition of $15 ml$ standard solution. Calculate the atomic mass of babaorum!
Answer
$n_{HCl}$ $=$ $0.2\cdot 0.015$ $=$ $0.003 mol$ One mole $HCl$ reacts with $\frac{1}{2}$ mole $Bb(OH)_2$: $n_{Bb(OH)_2}$ $=$ $0.0015 mol$ $M_{Bb(OH)_2}$ $=$ $\frac{m_{Bb(OH)_2}}{n_{Bb(OH)_2}}$ $=$ $\frac{0.257}{0.0015}$ $=$ $171.33\frac{g}{mol}$ $M_{Bb}$ $=$ $171.33$ $-$ $2(16+1)$ $=$ $137.33\frac{g}{mol}$