Säure-Base Titrierung
Tutorial 18
pH-Wert beim Titrieren einer schwachen Säure mit einer starken Base
Schema
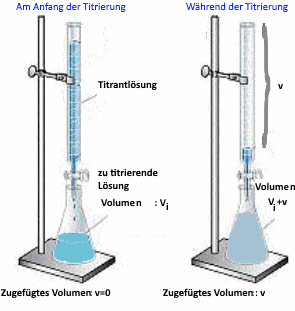
Bestimmung des Basenvolumens $ V_e $, das am äquivalenten Punkt (P.E.) hinzugefügt wird
Zum P.E.:
$ n_{hinzugefügte\; Base } = n_{Säure \; am \; Anfang} $
$ V_e \cdot c_{Base} = V_i \cdot c_{Säure} $
daher $ V_e $
pH basierend auf dem hinzugefügten $ v $ Basenvolumen
$ v = 0 $
pH-Wert einer schwachen Säure der Molarität $ c_{Säure} $:
$x=[H_3O^+]$
$x^2+c_{Säure}x-c_{Säure}K_a=0$
etc ..
$ v \lt V_e $
Bestimmen Sie die Anzahl der Mole der schwachen Säure $ n_a $, die noch nicht reagiert haben, und die Anzahl der Mole der gebildeten Base $ n_b $.
pH-Wert eines Puffers
$pH=pK_a+log\frac{n_b}{n_a}$
$ v = V_e $
pH-Wert einer schwachen Base der Molarität $ c_b $:
Die Molzahl der zu diesem Zeitpunkt vorhandenen schwachen Base ist $ n_b $ $ = $ $ n_ {hinzugefügte\; Base } $ $ = $ $ n_ {Säure \; am \; Anfang} $
Dann gilt: $ c_b = \frac{n_b}{V_i + V_e} $
dann
$ x = [OH^-] $:
$ x^2 + c_bx-c_bK_b = 0$
usw ..
$ v \gt V_e $
Bestimmen Sie die Anzahl Mole $ n_b $ der starken Base im Ãœberschuss
$ pH = 14 + log \frac{n_b}{V_i + v} $
$20\;mL\; HF \;0,10 \;M$ werden mit $KOH\;0,050\;M$ titriert. Berechnen Sie den pH-Wert nach Zugabe von $50\;mL\;KOH$.
Berechnen Sie zuerst das am P.E. hinzugefügte Volumen:
Für Antworten verwenden Sie die Pfeile ↑ und ↓ oben!
Beenden Sie bitte diese Frage, bevor Sie zur nächsten übergehen!
$V_e$ $=$ $\frac{0,020\cdot 0,10}{0,05}$ $=$ $40\;mL$
In welchem ​​Bereich der Titration befinden wir uns und wie wird die Berechnung durchgeführt ?
Berechnen Sie die Anzahl der Mole $ n_b $ der starken Base im Übermaß!
Ein Mol Säure reagierte mit einem Mol Base:
$n_b$ $=$ $n_{Base\;hinzugefügt}$ $- $ $n_{Säure\;am\;Anfang}$
$n_b$ $=$ $0,050\cdot0,050$ $- $ $0,020\cdot0,10$ $=$ $5\cdot 10^{-4}\;mol$
Berechnen Sie die Molarität $ c_b $ der Base!
$c_b$ $=$ $\frac{n_b}{V_i+v}$
$c_b$ $=$ $\frac{5\cdot 10^{-4}}{0,070}=7,14\cdot 10^{-3}\;M$
Berechnen Sie den pH-Wert!
Starke Base:
$pH$ $=$ $14+log\;c_{b}$
$pH$ $=$ $14+log\;7,14\cdot 10^{-3}$ $=$ $11,9$
